Games101: Computer Graphics-Week 4

Recap and supplement

• 对于旋转变换，逆时针旋转θ角度和顺时针旋转θ角度的矩阵恰好为正交矩阵，此时矩阵的转置和矩阵的逆相等。

• 为了统一平移变换和线性变换的书写形式，引入齐次坐标的概念，实质是增加一个维度；

3D Transformations

On homogeneous coordinates, 3D points/vectors can be described as :

• 3D point = $ (x, y, z, 1)^T$
• 3D vector = $ (x, y, z, 0)^T $
• In general, if $ (x, y, z, w)^T $ ($ w \neq 0$ and $w \neq 1$), which refers the same point $(x/w, y/w, z/w, 1)^T $

Scale

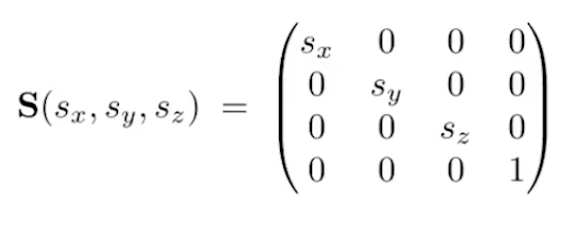
Translation

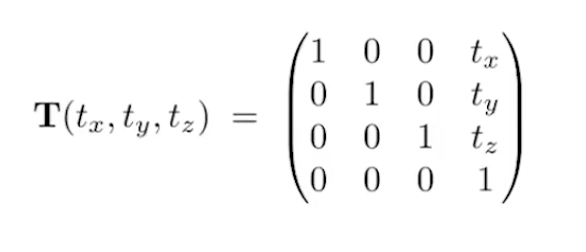
Rotate

先从绕某一固定轴进行旋转，更普遍的旋转是这三种旋转矩阵的连乘组合

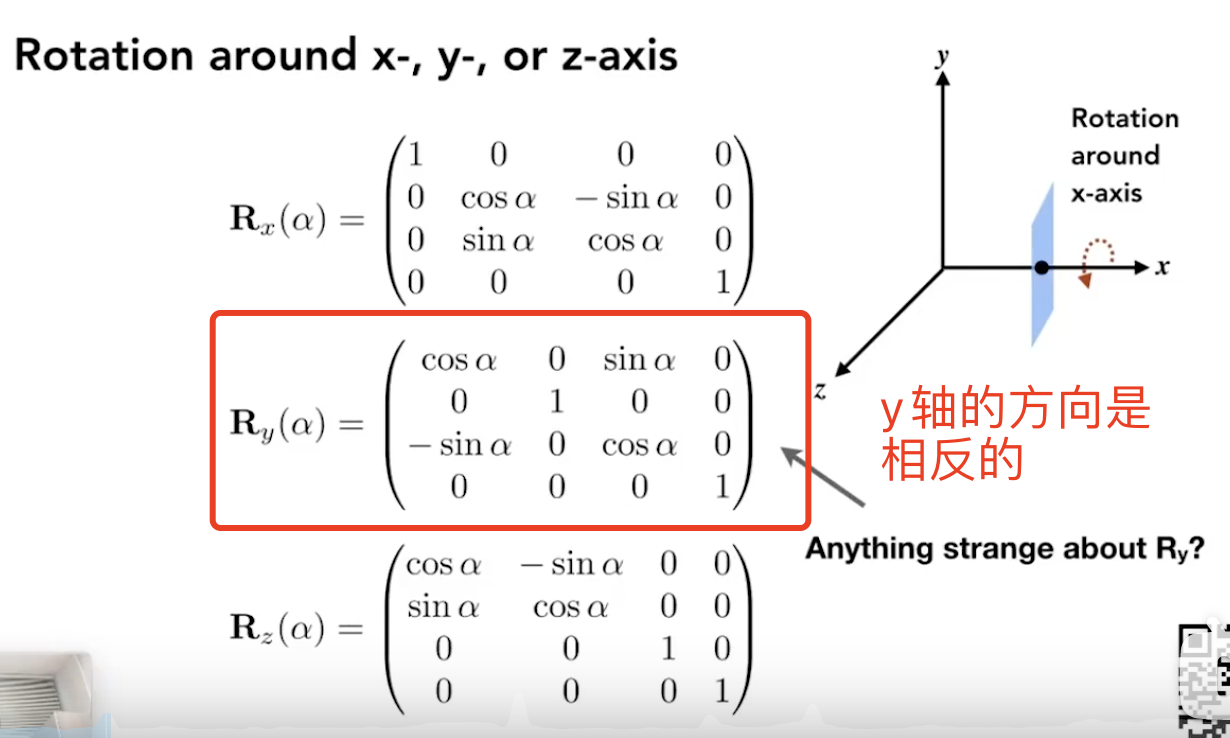
1. 怎么理解绕y轴旋转矩阵是反向的？

从坐标系可以看出：$ \vec{z} \times \vec{x} = \vec{y} $，而这里的坐标向量是按xyz组织的，$\vec{x}$与$\vec{z}$的顺序与坐标系规定恰好相反，所以方向是反的。

2. Rodrigues’ Rotation Formula(罗德里格斯旋转公式)

给定旋转角度α和旋转参考轴 $\vec{n}$ (默认旋转轴的起点是原点)，那么有如下公式：

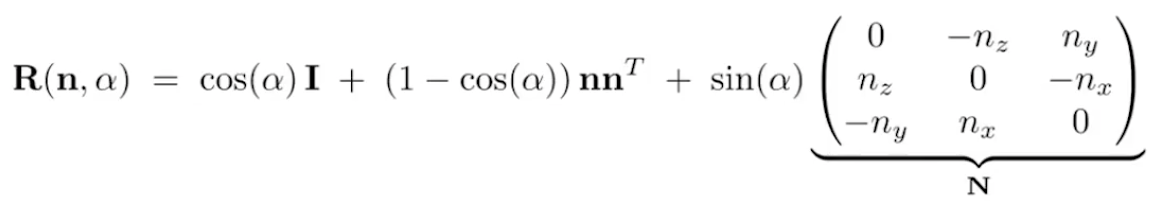
公式核心是将旋转分解到 $ \vec{x}, \vec{y}, \vec{z} $ 三个方向，然后进行旋转。公式$R(n, \alpha)$ 返回的是一个变换矩阵，上面的变换矩阵$ N $ 可以理解为两个向量做叉乘时，第一个向量可以改写为矩阵形式，进行左乘。

3. 在Rodrigues公式下，如何绕任意轴进行旋转？

先平移到原点，再套用公式进行旋转，然后再平移回旋转点。

略去概念：四元数，其引入目标是解决，旋转矩阵不能直接作线性插值。E.g. 一个旋转$\alpha$角度的矩阵A和旋转$\beta$角度的矩阵B，两矩阵相加除以2所得到的的矩阵不等于旋转$ (\alpha + \beta)/2$的矩阵，不是线性插值。

Viewing(观测) transformation

核心将三维图形变换到二维，两要素：三维场景+给定观察点；

类比拍照，给出View的三个步骤：

1. (Model transformation) Find a good place and arrange people - 设置好被摄影物体；
2. (View transformation) Find a good “angle” to put the camera - 找好相机角度；
3. (Projection transformation) Cheese! - 拍照；

上述三步合称为MVP变换，not means Most Valuable Players，下面主要介绍View transformation。

View(视图)/Camera transformation

1. How to perform view transformation?

备注：

• 位置向量$ \vec{e} $ ，观测方向 $ \vec{g}$，向上方向$ \vec{t}$(相机本身可以围绕观测方向旋转，因此需要指明方向，固定这个自由度)
• 考虑相对性，只有当物体和相机发生相对位移，摄像机的内容才会发生变化。因此，为了方便起见，这里惯例设定：相机放置在坐标系原点$(0, 0, 0)$，向上方向是沿$\vec{y}$，摄像机方向是$\vec{-z}$。

综上，核心是：将摄影机平移放置到原点，然后再将坐标系的不同轴旋转到标准的 $\vec{x}, \vec{y}, \vec{z}$ 方向：

注意：这里的旋转矩阵本身很难求，但可以逆向思考求解，以$\vec{x}=(1,0,0,0)^{T}$为例，将其旋转到$\vec{g}\times\vec{t}$方向，很容易写出$R_{view}^{-1}$的第一列，即$\vec{g}\times\vec{t}$在$\vec{x}, \vec{y}, \vec{z}$ 的分解向量，然后对$R_{view}$就是$R_{view}^{-1}$的转置！(旋转矩阵是正交矩阵的性质！！！)

Projection(投影) transformation

• 3D -> 2D；
• 分为正交投影和透视投影，区别在于投影图是否考虑了透视关系-近大远小；

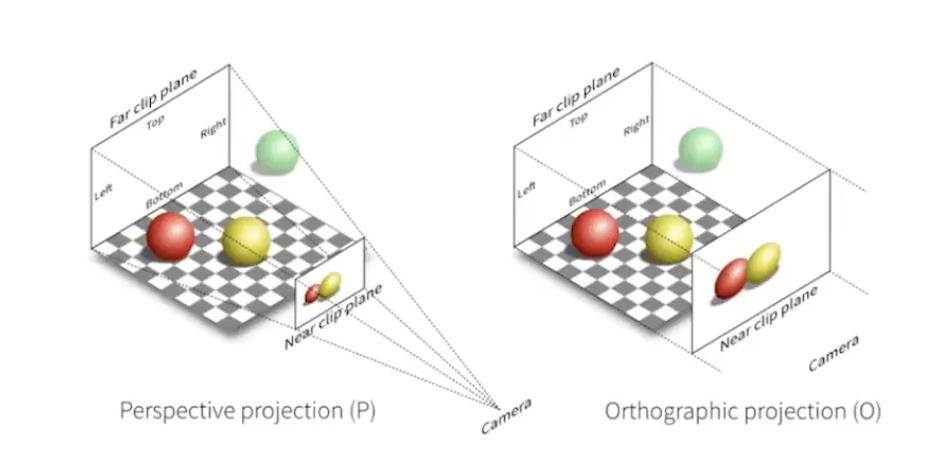
透视投影会汇聚于1个点，而正交投影可以认为相机在无限远处。

Orthographic projection-正交投影

理论步骤：

• 将相机(观测点)摆放到原点，方向设为惯例：看向$-\vec{Z}$，上方向为$\vec{Y}$;
• 物体点的坐标直接丢掉Y轴就可以了(这里要考虑前后重叠的问题)；
• 进行translate，再scale将投影放缩到$[-1,1]^2$(这里的上标2表示x和轴均为此范围)

实际步骤：

translate + scale

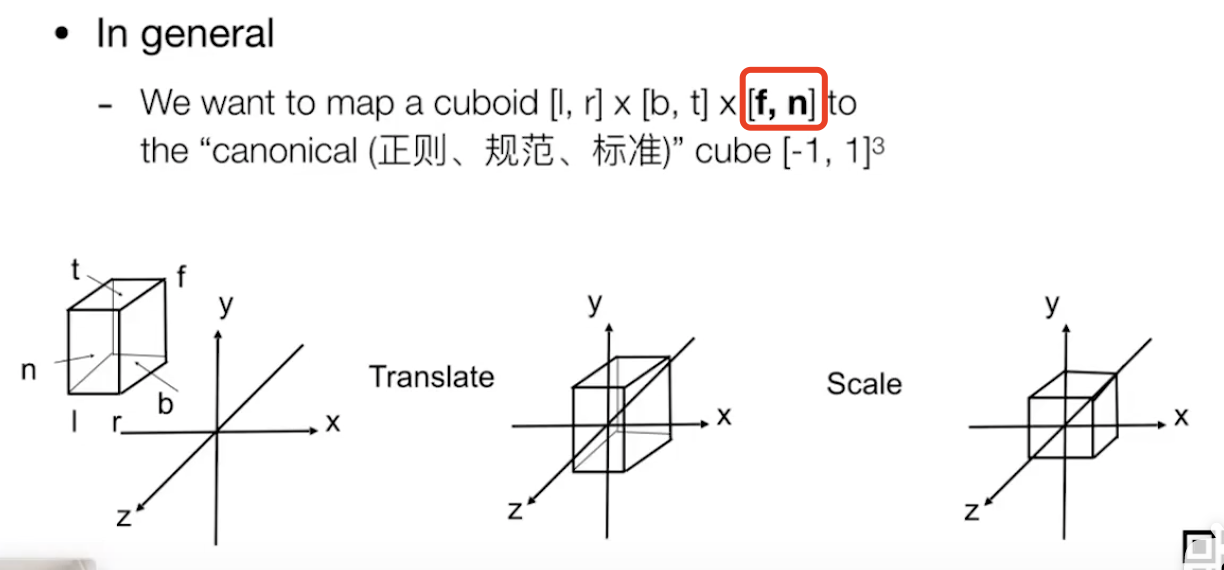
为什么是[f,n]而不是[n,f]?

注意相机观测是 $-y$方向，远点f的值小于近点n的值。

给出变换矩阵$M_{ortho}$：

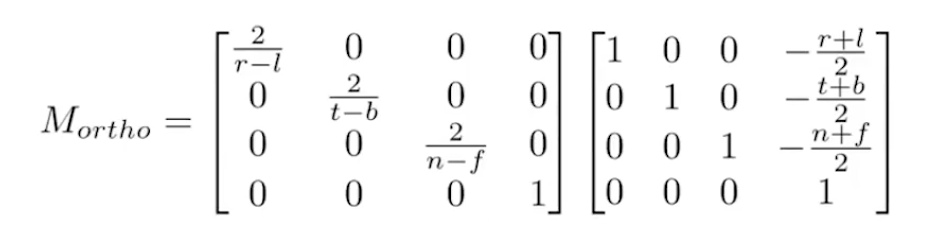
从矩阵可以看出，先平移到立方体中心，然后再缩放。

Perspective projection-透视投影

透视投影可以等效为两步：

1. 先将远点f在本平面内挤压，$M_{persp->ortho}$

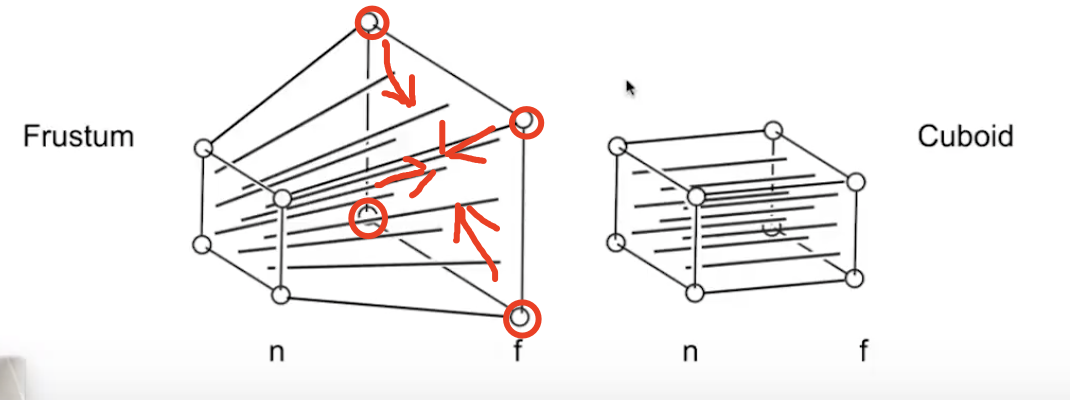
如图所示，将一个frustum(截头锥体)转换为Cuboid(立方体)

2. 再进行正交投影，$M_{ortho}$

因此，可以有两个结论：

1. 近平面n上的点应不受$M_{persp->ortho}$操作影响，远平面f上的点只在本平面内压缩，即点坐标$z$值布标；
2. 注意，这里并没有限制n和f之间的点在挤压操作后，z坐标不变！

所以，核心问题转为如何求$M_{persp->ortho}$？

1. 由透视关系，相似性原理可知：

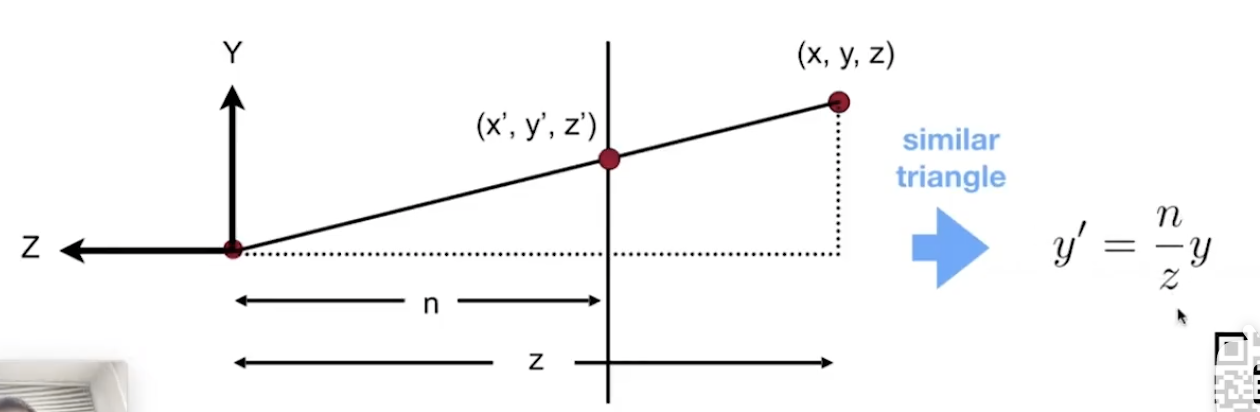
所以，对于任意点坐标(不局限n和f平面)：$(x,y,z,1)$有：

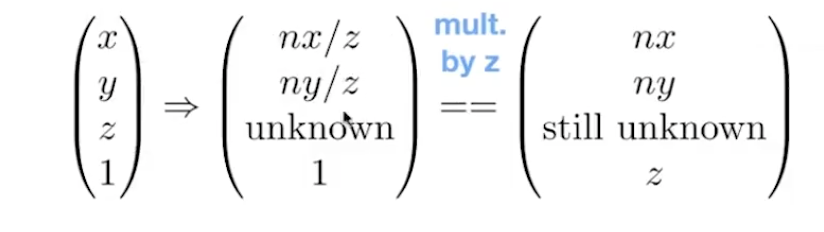
可知（待求z坐标的变换行向量）：

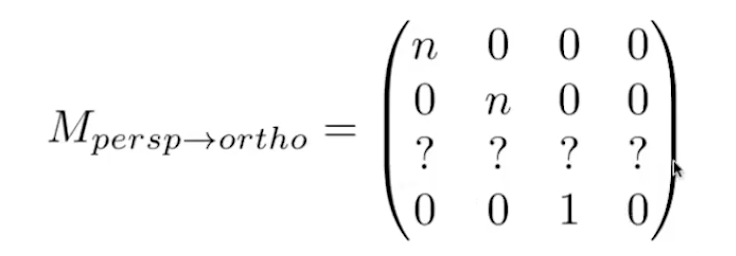
2. 引入n平面和f平面的预设关系(n平面上任意一点变换前后应不发生变化, f平面上的中心点变换前后应不发生变化)，列出方程组：

可以解得A和B，得到最后的透视投影的转换矩阵$M_{persp->ortho}$