Games101: Computer Graphics-Week 3

1. Transformation-变换

• Modelling-模型变换

  • 游戏中场景的变化；
  • 机器人跳舞（姿态变化）；
  • 物体相互作用发生形变和缩放；
  • 光栅化成像，从3D到2D的projection（投影）

• Viewing-视角变换

  同一个对象，主摄影视角进行变换产生不同的光栅化视角；

2. 2D Transformation

作为3维变换的基础，从2D变换讲起，核心是：将变换操作与矩阵操作联系起来！

Attention:

• 这些变换均可以由一个变换矩阵表征，所以统称为线性变换（Linear Transforms）；

• 下面的x, y为图上任意一点的坐标；

• 下面的变换默认是对基向量（单位长度）进行变换的；

2.1 Scale

• 等比缩放

• 非等比缩放

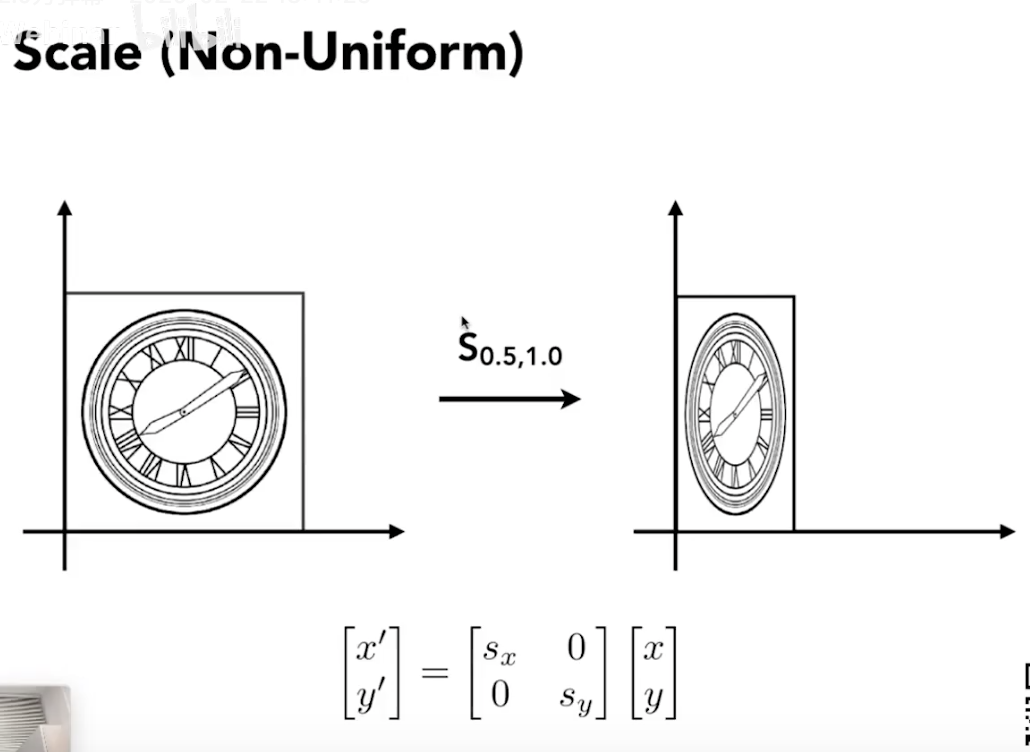
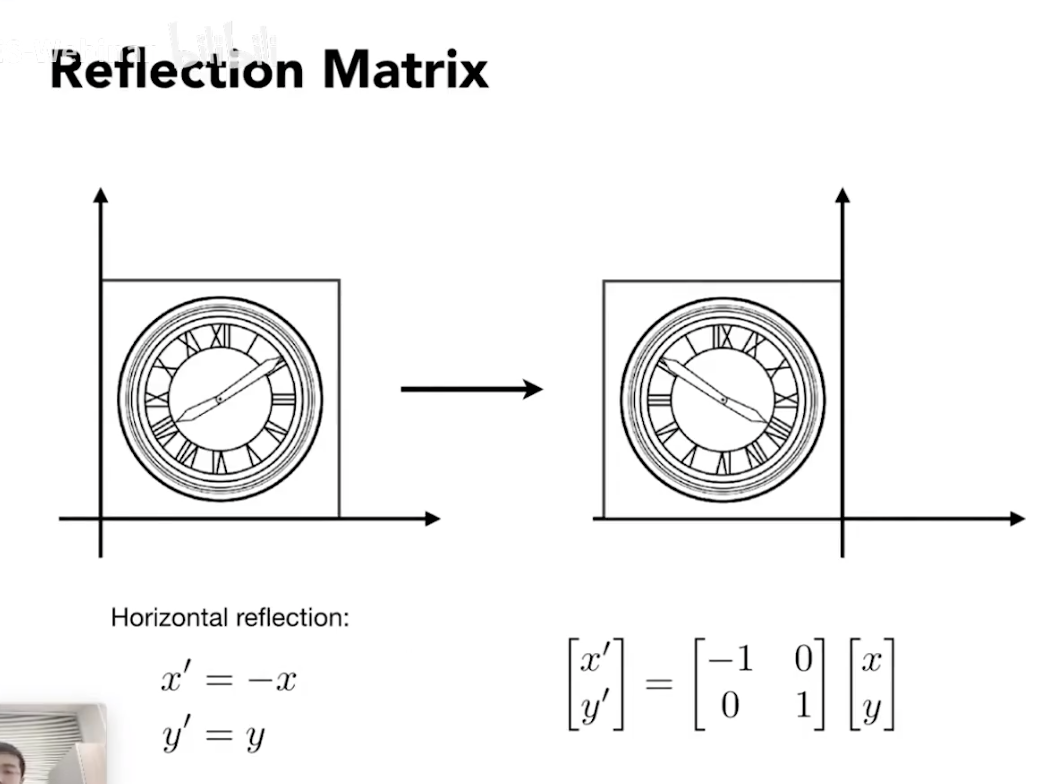
2.2 Reflection-翻转

以相对y轴进行镜像翻转为例，给出Reflection Matrix

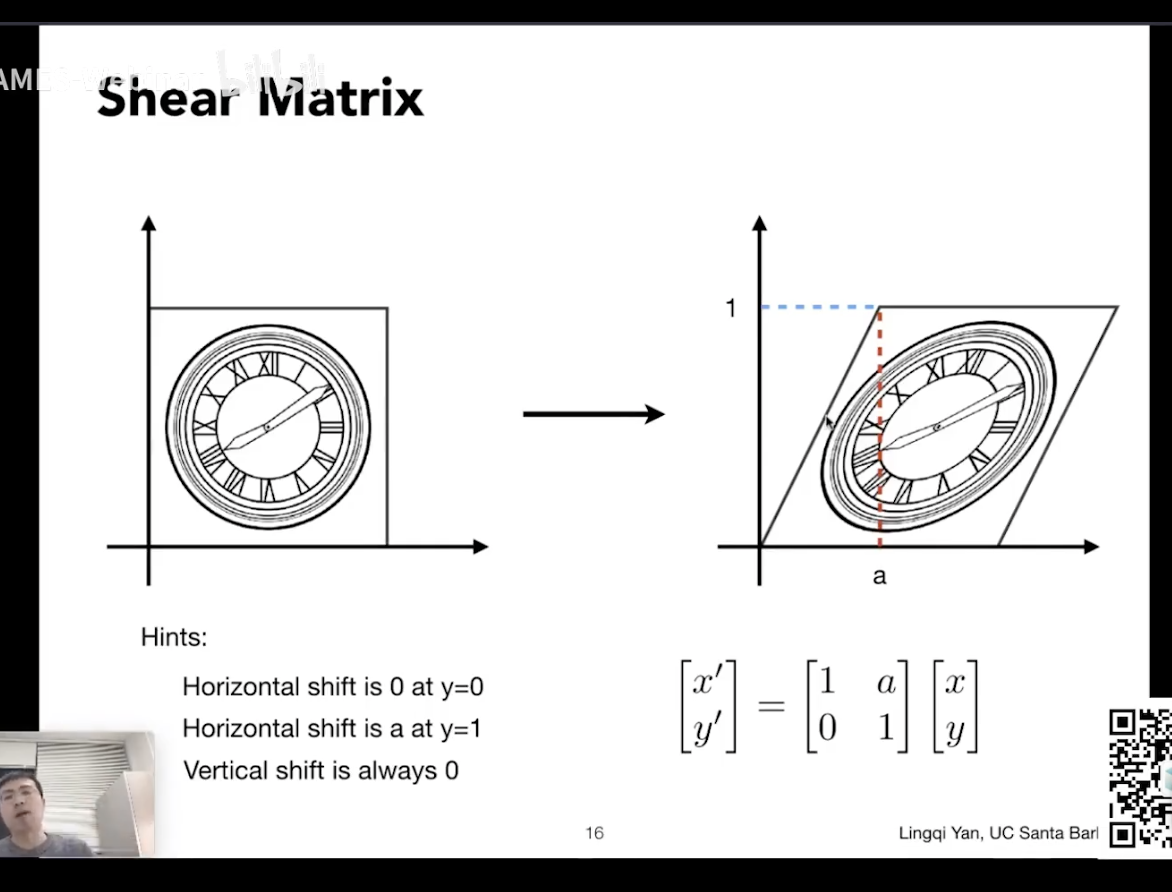
2.3 Shear-切变

物体具有一定的弹性，可以沿某个方向发生一定的形变。

2.4 Rotate-旋转

2D 旋转，默认逆时针以原点作为中心进行旋转

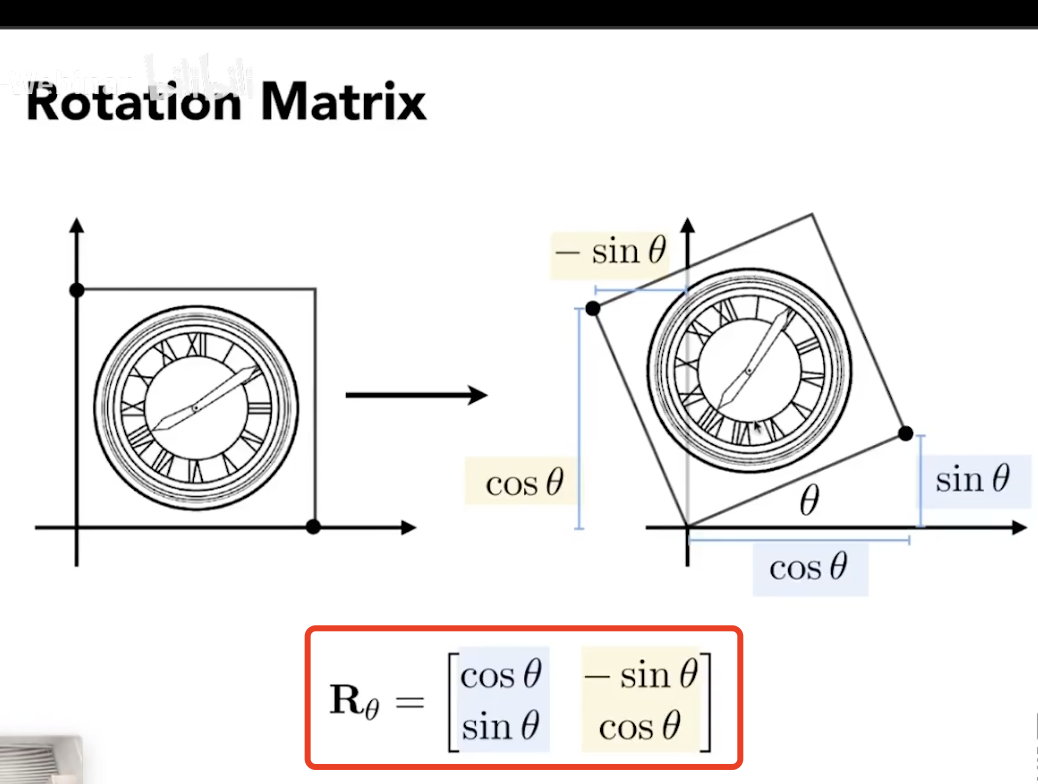
旋转矩阵的推导和证明：

• 法1：可以在旋转坐标系中，任选两个点求解映射变换表达式；
• 法2： 可以取两个特殊点(1,0)和(0,1)以逆时针旋转θ角度，根据旋转前后的坐标，列出4个方程，求解旋转矩阵的未知数；

2.5 Inverse Transform

逆变换矩阵就是原变换矩阵的逆矩阵。

Homogeneous Coordinates(齐次坐标)

• 上述的都是线性变换，可以表示为变换矩阵相乘的形式；

• Why引入齐次坐标？

当发生平移变换(Translation，就是翻译这个单词)时，无法再使用上面的变换矩阵相乘的形式进行表征，只能写作**仿射映射(Affline Map)**形式：

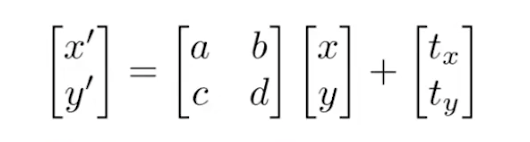
仿射变换 = 线性变换 + 平移（即便在齐次坐标中也是如此，先线性再平移）

由于这种形式不满足上面的方程形式，所不是线性变换。

为了能用上面的矩阵乘法形式统一表征变换操作，引入齐次坐标系的概念。

• 齐次坐标的定义

  • 点和向量的表示

    • 2D Point: $(x, y, 1)^T$

  • 2D Vector: $ (x, y, 0)^T$

• 平移变换表示

  

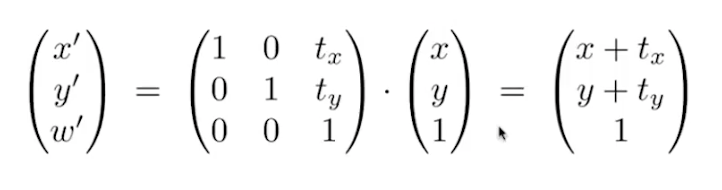
1. 为什么点的增加列为1，而向量的增加列为0？

• 首先，向量具有平移不变性，也就是说平移操作不应该影响向量；
• 其次，更深层次，这个符合物理定义：

在扩充定义的补充下，对于$ w \neq 1$的点，都进行归一化操作，此时point+point实际结果就是中点。

综上，可以用齐次坐标下的线性变换形式表示二维情况下的仿射变换时，齐次坐标的最后一行一定为$ (0, 0, 1) $。（注意限定条件，其他情况下，最后一行有意义）