Games101: Computer Graphics-Week 2

1. Vector-向量

课程中所有的向量默认是列向量形式，转置后为行向量；

1.1 Dot Production

在图形学中，核心的作用有三个：

1）求出两个向量的夹角，余弦值；

2）求出向量a在向量b上的投影，以及获得副产物法向量：

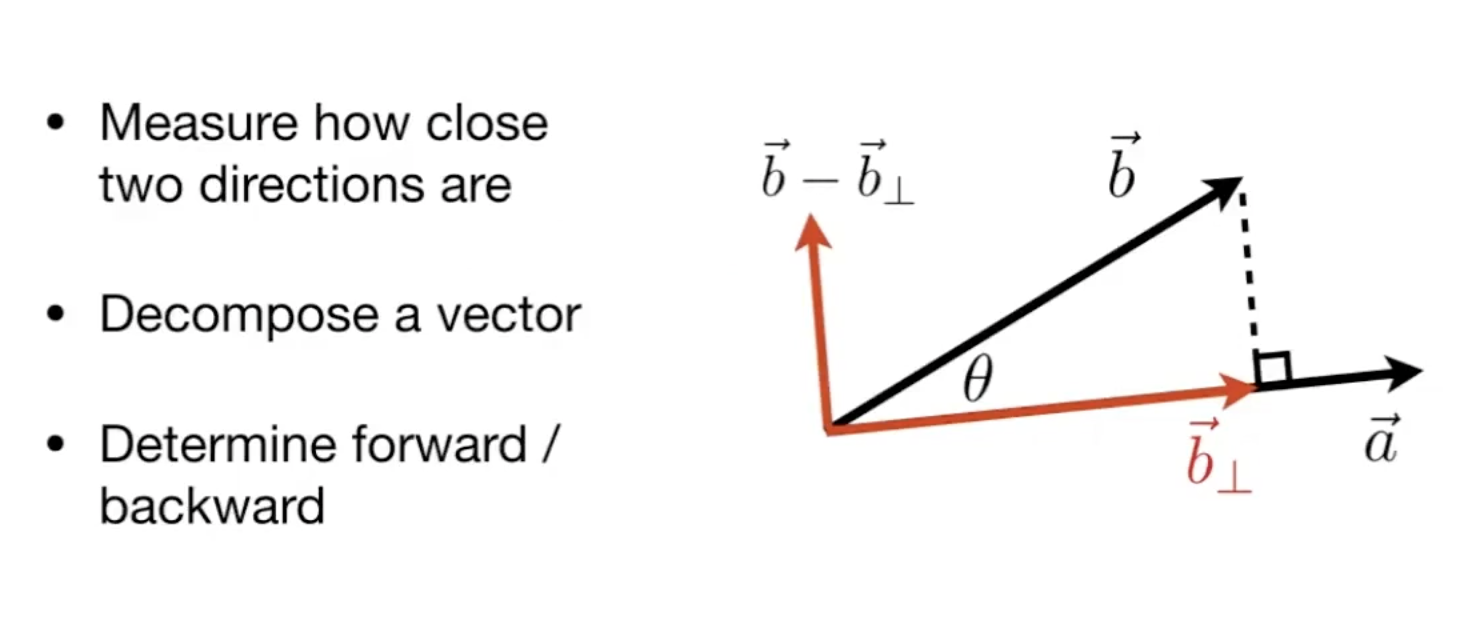
3）判断不同向量的前后关系（余弦相似度）：

这里的前后关系可以理解为**同向与反向**，而且这种关系应用于渲染的光线的金属高光反射参数。

1.2 Cross Production in Graphics

默认使用右手螺旋定则，与OPENGL一致，坐标系为右手系；

DirectX默认为左手系，即满足：
$$
\vec x \times \vec y = -\vec z
$$

在图形学中，叉乘主要有两个用处：

1）判断向量的左右

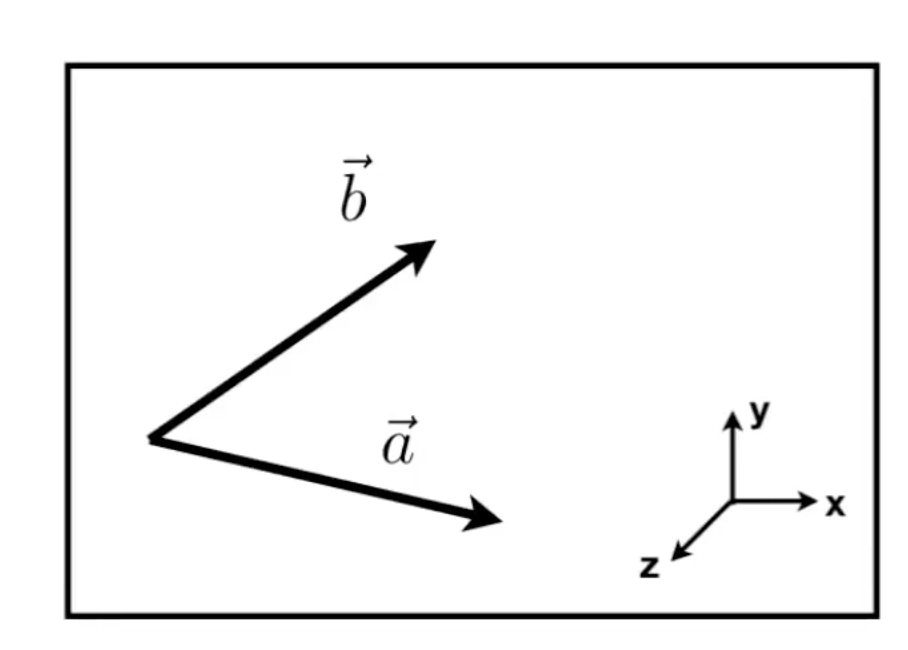
从右下角的示例可以看出，这是一个标准的右手系，有：
$$
\vec b \times \vec a <0, \vec a \times \vec b >0
$$
这时，对应关系为b在a的左侧，a在b的右侧。

2）判断点是否在图形内部

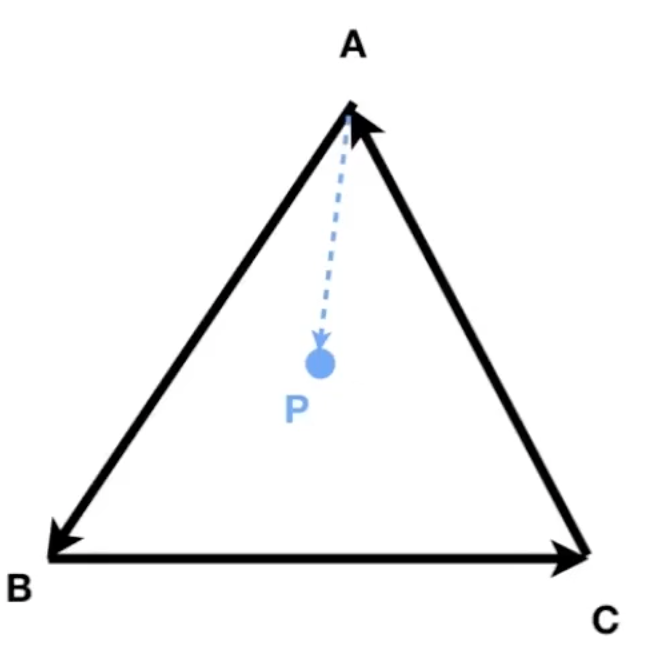
如何判断P在ABC的内部？

利用起那一步的左右性进行判断，以A->B->C顺序：
$$
\vec {AB} \times \vec {AP} >0, \vec {BC} \times \vec {BP}>0, \vec {CA} \times \vec {CP} >0
$$
可以看到，无论对于哪条边，点P始终在该边的左侧，因此P点在ABC中；

进一步，通用的结论是，无论ABC是顺时针，还是逆时针，若P点在图形内，则必然各边叉乘结果同号；反正，至少有一条边结果不同号则在外。

在边上的点，叉乘为0，corner case，是否包含该点由自己定义。

2. Matrix-矩阵

基础知识，矩阵的乘法解释挺有意思，贴在下面：

以及如何将向量的点乘和叉乘写成矩阵形式：