在依次进行了前面的步骤：

• Model transformation，将物体和摄像机放到标准位置； (M)

• View/Camera transformation，将摄像机角度到标准位置；(V)

• Projection Transformation，将被观测场景投影到标准的$[-1, 1]^{3}$范围后；(P)

After MVP transformation，下一步就是将Projection画在屏幕上，这一步就是Rasterization(光栅化) ！

Rasterization

Preview

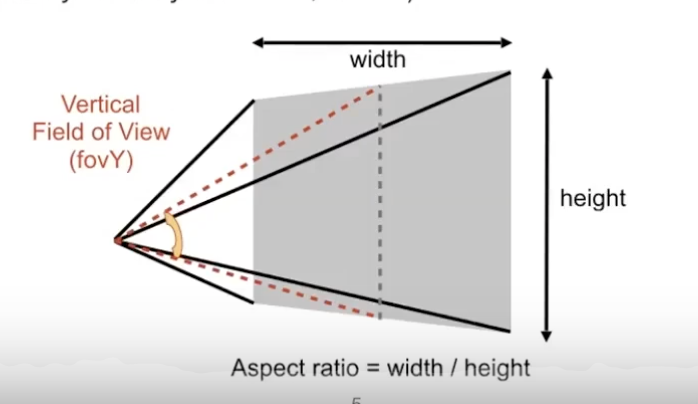
回顾上节课的定义，定义一个立方体需要知道：$x$轴上$[l,r]$，$y$轴上$[b, t]$，$-z$轴上$[f, n]$，这里假设我们已经知道$f$和$n$平面，对于Perspetive Projection而言，需要定义视角锥。如下图所示，定义近平面需要两要素：

1. Field-of-view(fovY，默认是垂直视角)：定义为两条横边中点的连线夹角，如图中两条红色虚线所示；
2. Aspect ratio(宽高比)： $Aspect ratio = width/height$；

• 类似垂直视角，可以定义水平视角，此时为两条竖边的中点，并且当固定了宽高比和Fov后，即可求出水平视角。
• 用相机类比，Fov可以对应镜头的焦距所对应的视角；

Canonical Cube to Screen

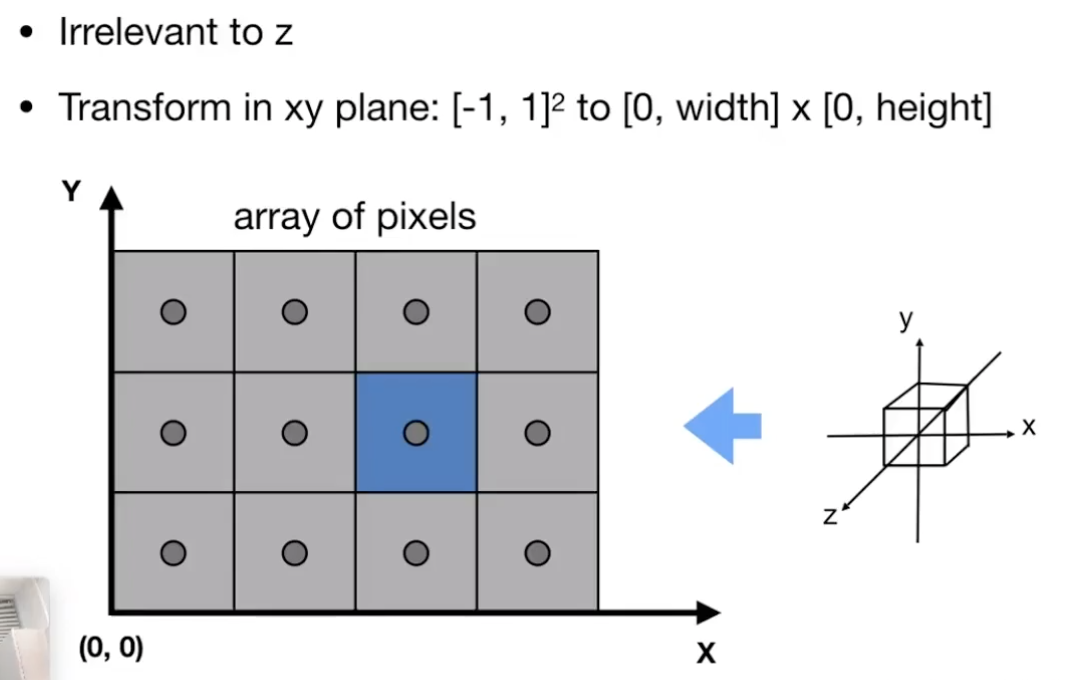
• 暂时不管$z$轴；
• 将MVP变换后的$[-1,1]^{2}$映射到$[0,width]\times[0,height]$尺寸上；
• 如何实现？先scale再translate；

注意在上述操作中，这些操作都是对空间中的各种立方体操作的，如何将这些立方体打散到每个像素点，求解到每个像素点像素值，这个过程称为光栅化。

Different raster displays(光栅显示设备)

• Oscilloscope(示波器)，显示原理和早期显示器一致，阴极射线管发生电子打到荧光屏上，CRT(Cathode Ray Tube)，以扫描的形式进行画图呈像；
• Frame Buffer，现在显示认为就是内存或显存中的一部分空间，屏幕就是讲内存中的内容映射显示到物理设备上，包括：
  • LCD(Liquid Crystal Display，液晶显示器)，利用液晶材料的极化作用，进行光线的扭转；
  • LED(Light Emitting Diode，发光二极管)；
  • Electronic Ink Display，电子墨水屏，刷新率很低；

Triangles - Fundamental Shape Primitives

重心坐标插值-barycentric interpolation

Rasterizing a triangle

光栅化最核心的步骤：

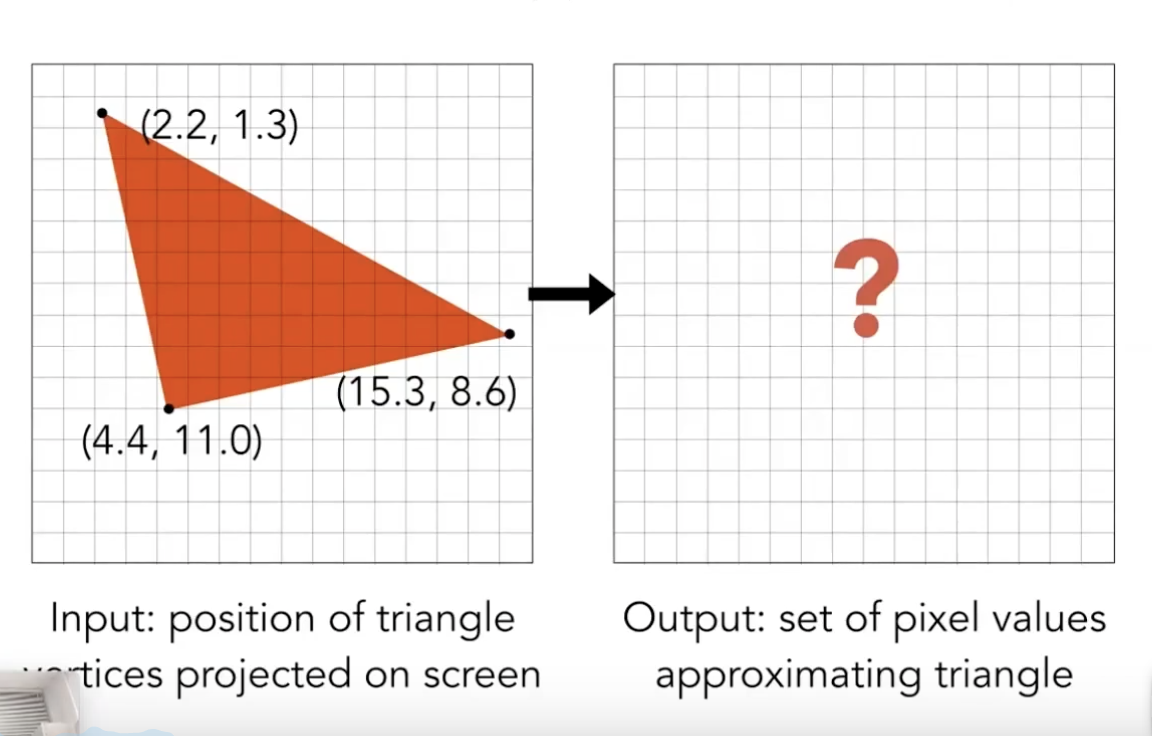
左图三角形代表经过MVP，Projection变换后的图形，图中每一个方格代表一个像素，光栅化就是判断每一个点和三角形的关系并进行取值。

下面介绍一个最简单和最广泛使用的方法-**采样(Sample)**：

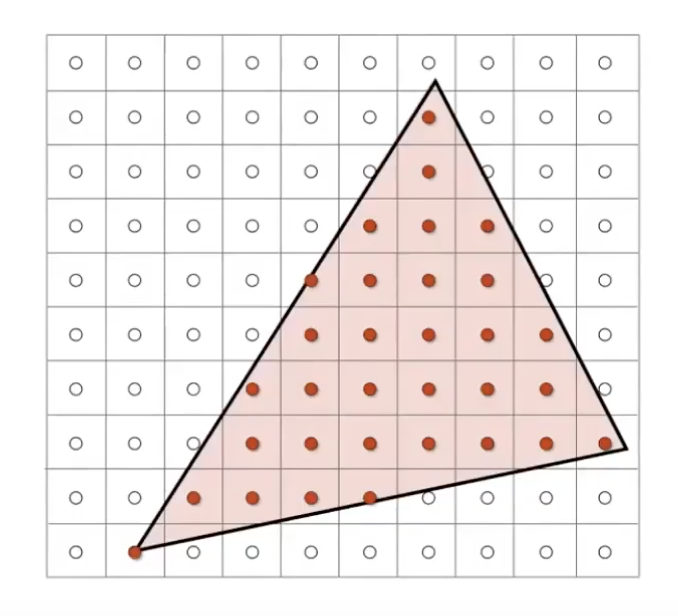
前提：

• 认为每个像素内部是不可分割，颜色一致的小块；
• 认为每个像素块的中心是$(x+0.5, y+0.5)$，由质心确定对应像素块的颜色；

这里用代码更容易说清楚：

1
2
3
4

for (int x=0; x<xmax; ++x)
  for(int y=0; y<ymax; ++y)
    // 这里的inside函数用以判断点是否在图形内侧，算法可参考前面的固定方向叉乘
    image[x][y] = inside(tri, x+0.5, y+0.5);

Recap and supplement

• 对于旋转变换，逆时针旋转θ角度和顺时针旋转θ角度的矩阵恰好为正交矩阵，此时矩阵的转置和矩阵的逆相等。

• 为了统一平移变换和线性变换的书写形式，引入齐次坐标的概念，实质是增加一个维度；

3D Transformations

On homogeneous coordinates, 3D points/vectors can be described as :

• 3D point = $ (x, y, z, 1)^T$
• 3D vector = $ (x, y, z, 0)^T $
• In general, if $ (x, y, z, w)^T $ ($ w \neq 0$ and $w \neq 1$), which refers the same point $(x/w, y/w, z/w, 1)^T $

1. Transformation-变换

• Modelling-模型变换

  • 游戏中场景的变化；
  • 机器人跳舞（姿态变化）；
  • 物体相互作用发生形变和缩放；
  • 光栅化成像，从3D到2D的projection（投影）

• Viewing-视角变换

  同一个对象，主摄影视角进行变换产生不同的光栅化视角；

1. Vector-向量

课程中所有的向量默认是列向量形式，转置后为行向量；

1.1 Dot Production

在图形学中，核心的作用有三个：

1）求出两个向量的夹角，余弦值；

2）求出向量a在向量b上的投影，以及获得副产物法向量：

3）判断不同向量的前后关系（余弦相似度）：

1. Why study Computer Graphics?

• Applications: Video Games, Movies, Animations, Design, Visualization, VR&AR, Digital Illustration, Simulation, GUI, Typography
• Fundamental Intellectual Challenges
  • Creates and interacts with realistic virtual world
  • Requires understanding of all aspects of physical world
  • New computing methods, displays, technologies
• Technical Challenges
  • Math of (perspective) projections, curves, surfaces
  • Physics of lighting and shading
  • Representing / operating shapes in 3D
  • Animation / simulation
  • 3D graphics software programming and hardware

课程主要资料

• 课程录播-Video Lecture

• 课件-PowerPoints

• 课程笔记-Lecture Notes

• 课后作业-Homework

• 推荐教材及读物

  • (Tiger book)

Lecture Notes

• Lec 01 - Overview 计算机图形学概述+专业名词解释
• Lec 02 - Linear Algebra 必备的向量和线性代数知识
• Lec 03 - Transformations 基础的2D变换和齐次坐标系

Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub.